” A calibração garante uma boa medição.” 😉

Para ilustrar melhor as definições acima, vamos tomar como exemplo a medição de um lápis utilizando-se uma régua.

• GRANDEZA -> comprimento  –  grandeza dimensional
• MENSURANDO -> lápis
• SISTEMA DE MEDIÇÃO -> nesse caso é o próprio instrumento de medição -> régua
• MÉTODO DE MEDIÇÃO -> medição direta (faz-se a leitura diretamente no instrumento de medição)
• RESULTADO DA MEDIÇÃO -> no exemplo o valor medido é 136 mm, o resultado deve ser expresso numericamente e ter uma unidade de medida rastreável ao SI (Sistema Internacional de Unidade).

  

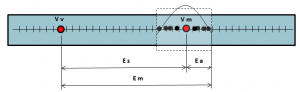
Quando fazemos uma série de medições com razoável exatidão de uma grandeza conhecida obtemos valores com uma determinada dispersão, conforme ilustrado na figura abaixo:

v -> Valor verdadeiro

Vm -> Valor médio (média entre todas as medidas realizadas)

Es -> Erro sistemático (Es = Vv – Vm)

Ea -> Erro aleatório (é determinado utilizando-se métodos estáticos)

Em -> Erro da medição

Valor verdadeiro:

Valor de uma grandeza compatível com a definição da grandeza.

NOTA 1 Na Abordagem de Erro para descrever as medições, o valor verdadeiro é considerado único e, na prática, impossível de ser conhecido. A Abordagem de Incerteza consiste no reconhecimento de que, devido à quantidade intrinsecamente incompleta de detalhes na definição de uma grandeza, não existe um valor verdadeiro único, mas um conjunto de valores verdadeiros consistentes com a definição. Entretanto, este conjunto de valores é, em princípio e na prática, impossível de ser conhecido. Outras abordagens evitam completamente o conceito de valor verdadeiro e avaliam a validade dos resultados de medição com auxílio do conceito de compatibilidade metrológica.

NOTA 2 No caso particular de uma constante fundamental, considera-se que a grandeza tenha um valor verdadeiro único.

NOTA 3 Quando a incerteza definicional, associada ao mensurando, é considerada desprezível em comparação com os outros componentes da incerteza de medição, pode-se considerar que o mensurando possui um valor verdadeiro “essencialmente único”. Esta é a abordagem adotada pelo GUM e documentos associados, onde a palavra “verdadeiro” é considerada redundante.

Erro sistemático:

Componente do erro de medição que, em medições repetidas, permanece constante ou varia de maneira previsível.

NOTA 1 Um valor de referência para um erro sistemático é um valor verdadeiro, ou um valor medido de um padrão com incerteza de medição desprezível, ou um valor convencional.

NOTA 2 O erro sistemático e suas causas podem ser conhecidos ou desconhecidos. Pode-se aplicar uma correção para compensar um erro sistemático conhecido.

NOTA 3 O erro sistemático é igual à diferença entre o erro de medição e o erro aleatório.

 Erro aleatório:

Componente do erro de medição que, em medições repetidas, varia de maneira imprevisível.

NOTA 1 O valor de referência para um erro aleatório é a média que resultaria de um número infinito de medições repetidas do mesmo mensurando.

NOTA 2 Os erros aleatórios de um conjunto de medições repetidas formam uma distribuição que pode ser resumida por sua esperança matemática ou valor esperado, o qual é geralmente assumido como sendo zero, e por sua variância.

NOTA 3 O erro aleatório é igual à diferença entre o erro de medição e o erro sistemático.
“A Calibração evita erros nas medidas” 🙂